Probabilités
- Vous devez vous identifier ou créer un compte pour écrire des commentaires
jeu, 08/03/2012 - 09:55
A vos calculettes, j'en connais qui sont forts pour ce genre de calcul.
Table de 9 joueurs.
4 joueurs call la big blind.
Héro : As 5
Tirage flop : 7 As 5
Je veux juste savoir le pourcentage de probabilité que l'un des autres 3 autres joueurs ai une paire de 5.
Table de 9 joueurs.
4 joueurs call la big blind.
Héro : As 5
Tirage flop : 7 As 5
Je veux juste savoir le pourcentage de probabilité que l'un des autres 3 autres joueurs ai une paire de 5.
jeu, 08/03/2012 - 14:27
#2
j'avais pas vu 
du coup j'ose plus te parler de ton approximation contestable qui consiste a multiplier par le nombre de joueurs.
du coup j'ose plus te parler de ton approximation contestable qui consiste a multiplier par le nombre de joueurs.
jeu, 08/03/2012 - 14:37
#3
J'ai été un peu lent sur ce coup
Dynax tu t'en sors bien grâce aux arrondies.. Bien vu kali !!
kaliganzaris a écrit :
j'avais pas vu
du coup j'ose plus te parler de ton approximation contestable qui consiste a multiplier par le nombre de joueurs.
Dynax tu t'en sors bien grâce aux arrondies.. Bien vu kali !!
__________________
Soutenez EFVI par votre signature - http://www.efvi.eu/index.fr.html
jeu, 08/03/2012 - 15:21
#4
kaliganzaris, en substance, a écrit :
[tu fais une] approximation contestable qui consiste a multiplier par le nombre de joueurs.
mmm...voyons voir :
il faut qu'il y ait un joueur sur les 3 qui ait la paire de 5 cela peut se faire de 3 façons différentes : soit c'est le 1er, soit c'est le 2eme, soit c'est le 3ème
donc 3 possibilités (et l'ordre ne compte pas). => 3* 1/1000.On peut le vérifier avec un calculateur de cote sur un board à 5 cartes où SEULE la paire de cinq fait gagner un des adversaires. Dans ce cas la probabilité pour avoir la paire de 5 est légèrement différente puisque c'est (1/45*1/44)*2 = 1.01 pour mille, mais le raisonnement est le même.
par exemple:
Hero :
Board :
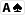
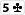
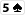
et on lance l'évaluation pour 1 adversaire, 2 adversaires... n adversaires et les résultats parlent d'eux mêmes: Héro perd bien 0.1% d'equity à chaque nouvel adversaire !
si je reprends mon script python (qui utilise un algo type "monte-carlo", comme "poker stove" par exemple), voilà ce qu'il me donne (je me suis amusé à aller jusqu'à 20 adversaires !).:
EVALUATION on board AS5C5S7DJH:
player1 ADAH : win=799193(99.899125%) tie=0(0.00%) EQUITY=99.90%
player2 XXXX : win=807(0.100875%) tie=0(0.00%) EQUITY=0.10%
EVALUATION on board AS5C5S7DJH:
player1 ADAH : win=598766(99.794333%) tie=0(0.00%) EQUITY=99.79%
player2 XXXX : win=604(0.100667%) tie=0(0.00%) EQUITY=0.10%
player3 XXXX : win=630(0.105000%) tie=0(0.00%) EQUITY=0.10%
EVALUATION on board AS5C5S7DJH:
player1 ADAH : win=498493(99.698600%) tie=0(0.00%) EQUITY=99.70%
player2 XXXX : win=504(0.100800%) tie=0(0.00%) EQUITY=0.10%
player3 XXXX : win=500(0.100000%) tie=0(0.00%) EQUITY=0.10%
player4 XXXX : win=503(0.100600%) tie=0(0.00%) EQUITY=0.10%
EVALUATION on board AS5C5S7DJH:
player1 ADAH : win=792039(99.004875%) tie=0(0.00%) EQUITY=99.00%
player2 XXXX : win=782(0.097750%) tie=0(0.00%) EQUITY=0.10%
player3 XXXX : win=779(0.097375%) tie=0(0.00%) EQUITY=0.10%
player4 XXXX : win=807(0.100875%) tie=0(0.00%) EQUITY=0.10%
player5 XXXX : win=803(0.100375%) tie=0(0.00%) EQUITY=0.10%
player6 XXXX : win=784(0.098000%) tie=0(0.00%) EQUITY=0.10%
player7 XXXX : win=804(0.100500%) tie=0(0.00%) EQUITY=0.10%
player8 XXXX : win=757(0.094625%) tie=0(0.00%) EQUITY=0.09%
player9 XXXX : win=779(0.097375%) tie=0(0.00%) EQUITY=0.10%
player10 XXXX : win=831(0.103875%) tie=0(0.00%) EQUITY=0.10%
player11 XXXX : win=835(0.104375%) tie=0(0.00%) EQUITY=0.10%
EVALUATION on board AS5C5S7DJH:
player1 ADAH : win=587880(97.980000%) tie=0(0.00%) EQUITY=97.98%
player2 XXXX : win=604(0.100667%) tie=0(0.00%) EQUITY=0.10%
player3 XXXX : win=600(0.100000%) tie=0(0.00%) EQUITY=0.10%
player4 XXXX : win=633(0.105500%) tie=0(0.00%) EQUITY=0.11%
player5 XXXX : win=610(0.101667%) tie=0(0.00%) EQUITY=0.10%
player6 XXXX : win=610(0.101667%) tie=0(0.00%) EQUITY=0.10%
player7 XXXX : win=587(0.097833%) tie=0(0.00%) EQUITY=0.10%
player8 XXXX : win=595(0.099167%) tie=0(0.00%) EQUITY=0.10%
player9 XXXX : win=563(0.093833%) tie=0(0.00%) EQUITY=0.09%
player10 XXXX : win=644(0.107333%) tie=0(0.00%) EQUITY=0.11%
player11 XXXX : win=564(0.094000%) tie=0(0.00%) EQUITY=0.09%
player12 XXXX : win=651(0.108500%) tie=0(0.00%) EQUITY=0.11%
player13 XXXX : win=611(0.101833%) tie=0(0.00%) EQUITY=0.10%
player14 XXXX : win=611(0.101833%) tie=0(0.00%) EQUITY=0.10%
player15 XXXX : win=617(0.102833%) tie=0(0.00%) EQUITY=0.10%
player16 XXXX : win=598(0.099667%) tie=0(0.00%) EQUITY=0.10%
player17 XXXX : win=579(0.096500%) tie=0(0.00%) EQUITY=0.10%
player18 XXXX : win=666(0.111000%) tie=0(0.00%) EQUITY=0.11%
player19 XXXX : win=585(0.097500%) tie=0(0.00%) EQUITY=0.10%
player20 XXXX : win=591(0.098500%) tie=0(0.00%) EQUITY=0.10%
player21 XXXX : win=601(0.100167%) tie=0(0.00%) EQUITY=0.10%
jeu, 08/03/2012 - 16:12
#5
pffffttttttttttt...même pas un petit pourcentage de good ou bad run ici....comme une vinaigrette sans moutarde, l'amour sans préliminaires...c'est vraiment que du terre à terre !
jeu, 08/03/2012 - 17:48
#6
juste une petite précision (au risque de choquer pilot encore un peu plus ), car en terme de probabilités, la précision des hypothèses de départ est primordiale :
quand je posais la question "quelle est la chance que Héro soit battu par une paire de 5", je voulais dire "quelle est la chance que Héro se retrouve en face d'une paire de 5 à ce moment du coup", car bien entendu, même si Héro est contre une paire de 5 au flop, il peut encore chatter les 2 as (en runner-runner) pour avoir le carré d'As.
J'ai émis cette hypothèse car je suppose que c'était le sens de la question de Sellig qui a du ramasser grave en partant à tapis avec sa double paire alors qu'un de ses adversaire avait déjà le carré... non ?
Et bien tu avais une chance sur 333 que ça t'arrive sellig!
alors, c'est pas du bad ça pilot !!??
PS: et pour être complet, la chance que Héro gagne le coup quand même si il est contre une paire de 5 au flop est de (1/45*1/44)*2 soit 1 pour mille.
), car en terme de probabilités, la précision des hypothèses de départ est primordiale :quand je posais la question "quelle est la chance que Héro soit battu par une paire de 5", je voulais dire "quelle est la chance que Héro se retrouve en face d'une paire de 5 à ce moment du coup", car bien entendu, même si Héro est contre une paire de 5 au flop, il peut encore chatter les 2 as (en runner-runner) pour avoir le carré d'As.
J'ai émis cette hypothèse car je suppose que c'était le sens de la question de Sellig qui a du ramasser grave en partant à tapis avec sa double paire alors qu'un de ses adversaire avait déjà le carré... non ?
Et bien tu avais une chance sur 333 que ça t'arrive sellig
!alors, c'est pas du bad ça pilot !!??
PS: et pour être complet, la chance que Héro gagne le coup quand même si il est contre une paire de 5 au flop est de (1/45*1/44)*2 soit 1 pour mille.
jeu, 08/03/2012 - 18:13
#7
DynaX a écrit :
juste une petite précision (au risque de choquer pilot encore un peu plus
quand je posais la question "quelle est la chance que Héro soit battu par une paire de 5", je voulais dire "quelle est la chance que Héro se retrouve en face d'une paire de 5 à ce moment du coup", car bien entendu, même si Héro est contre une paire de 5 au flop, il peut encore chatter les 2 as (en runner-runner) pour avoir le carré d'As.
J'ai émis cette hypothèse car je suppose que c'était le sens de la question de Sellig qui a du ramasser grave en partant à tapis avec sa double paire alors qu'un de ses adversaire avait déjà le carré... non ?
Et bien tu avais une chance sur 333 que ça t'arrive sellig
alors, c'est pas du bad ça pilot !!??
PS: et pour être complet, la chance que Héro gagne le coup quand même si il est contre une paire de 5 au flop est de (1/45*1/44)*2 soit 1 pour mille.
Je me doutais que tu allais réagir, mais je voulais quand même pas que tu y passes ton après midi
J'ai un peu du mal à y voir clair, mais il me semble qu'on est quand même dans un cas de probabilité composées.
si un évenement a 1 chance sur 1000 de se produire; la répétition 1000 fois de cet évenement ne donne pas une certitude.
Les shadoks avaient construit une fusée qui avait 1 chance sur 1 million de décoller. Alors ils se dépéchaient de rater les 999 999 premiers lancement pour enfin voir décoller leur fusée.
jeu, 08/03/2012 - 18:43
#8
T'as bien bossé dis donc!!Mais ça dit pas si les arrondies ne jouent pas des tours.
Juste histoire de chipoter parce que ça change pas grand chose au résultats de toute façon. Ça pique sellig hein
Bon sinon voilà ce que j'ai pensé:
Ici c'est la probabilité qu'un des trois joueur ait la pp5 qu'on calcule et pas la probabilité d'avoir reçu la pp5. C'est pour ça qu'à fois que qu'on calcule les probas pour un nouveau joueur il faut enlever 2 cartes:
Contre le 1 joueur:
Il a 2 cartes sur les 47 cartes non vues (52-3-2), soit:
47*46/2= 1081 combos possibles
Il reste un combo de 55
=>probabilité de 1/1081 ou 0.0925%
Contre le 2 joueurs:
Il a 2 cartes sur les 45 cartes non vues (47 - joueur1)
45*44/2= 990 combos possibles
=>probabilité de 1/990 ou 0.1010%
Contre le 3 joueurs:
Il a 2 cartes sur les 43 cartes non vues...
43*42/2=903 combos possibles
=>probabilité de 1/903 ou 0.1707%
J'ai la flème de finir les calculs mais on voit que la probabilité qu'un des 3 joueurs ait la pp5 augmente de façon non linéaire.
T'en penses quoi... Et toi kali?
__________________
Soutenez EFVI par votre signature - http://www.efvi.eu/index.fr.html
jeu, 08/03/2012 - 18:52
#9
kaliganzaris a écrit :
J'ai un peu du mal à y voir clair, mais il me semble qu'on est quand même dans un cas de probabilité composées.
si un évenement a 1 chance sur 1000 de se produire; la répétition 1000 fois de cet évenement ne donne pas une certitude.
Les shadoks avaient construit une fusée qui avait 1 chance sur 1 million de décoller. Alors ils se dépéchaient de rater les 999 999 premiers lancement pour enfin voir décoller leur fusée.
?? tu veux dire que si tu lances une pièce et qu'elle tombe sur face 750 fois sur 1000 lancés, on ne peut pas déduire que faire face, a une espérance de 75% ??
__________________
Soutenez EFVI par votre signature - http://www.efvi.eu/index.fr.html
jeu, 08/03/2012 - 19:01
#10
Koni, je pense que si ton calcul était bon, l'erreur serait suffisamment significative pour que l'évaluation sur 20 joueurs que j'ai fait avec l'ordi le montre.
si on pousse ton raisonnement pour 23 joueurs, le dernier touchera forcément la paire de 5 (ou quasi car le nombre de cartes est impair) et donc contre 23 adversaires, Héro serait toujours perdant !! (ce qui est évidemment faux, pas besoin de calcul pour ça) => dans ton raisonnement pour le joueur n, tu élimines systématiquement les 5 des mains des n-1 joueurs précédents, ce qui est une erreur...
si on pousse ton raisonnement pour 23 joueurs, le dernier touchera forcément la paire de 5 (ou quasi car le nombre de cartes est impair) et donc contre 23 adversaires, Héro serait toujours perdant !! (ce qui est évidemment faux, pas besoin de calcul pour ça) => dans ton raisonnement pour le joueur n, tu élimines systématiquement les 5 des mains des n-1 joueurs précédents, ce qui est une erreur...
jeu, 08/03/2012 - 19:56
#11
Stove te donne la probabilité de gain de A5 contre x joueurs avec un éventail random mais pas la probabilité de te retrouver face à 55.
Là ou on est d'accord c'est sur la probabilité, en hu que l'adversaire ait 55. Par contre contre 2 joueurs ou plus, la probabilité que l'un des deux ait 55 équivaut à la probabilité P(totale)=P(joueur1)*P(joueur2) reste à démontrer que P(joueur1)*P(joueur2)≠P(joueur1)*2
Edit: ?? j'enlève pas de 5 dans les calculs! euh non je retire 2 cartes pour le calcul du joueur n+1. Prenons l'exemple du joueur 2, il a reçu un seul 5, quand tu vas calculer la proba pour le joueur 3, tu fais le calcul en sachant que 2 cartes non vues, ont été donné. L'une d'elle peut être un 5 ce qui donne au joueur 3 une probabilité de 0 d'avoir 55.
Là ou on est d'accord c'est sur la probabilité, en hu que l'adversaire ait 55. Par contre contre 2 joueurs ou plus, la probabilité que l'un des deux ait 55 équivaut à la probabilité P(totale)=P(joueur1)*P(joueur2) reste à démontrer que P(joueur1)*P(joueur2)≠P(joueur1)*2
Edit: ?? j'enlève pas de 5 dans les calculs! euh non je retire 2 cartes pour le calcul du joueur n+1. Prenons l'exemple du joueur 2, il a reçu un seul 5, quand tu vas calculer la proba pour le joueur 3, tu fais le calcul en sachant que 2 cartes non vues, ont été donné. L'une d'elle peut être un 5 ce qui donne au joueur 3 une probabilité de 0 d'avoir 55.
__________________
Soutenez EFVI par votre signature - http://www.efvi.eu/index.fr.html
jeu, 08/03/2012 - 20:43
#12
Arretez les gars, sellig07 vient de faire une embolie cérébrale
ven, 09/03/2012 - 00:11
#13
ven, 09/03/2012 - 09:13
#14
Un évenement a une probabilité p
La non réalisation de l'évènement a une probabilité (1-p)
La non réalisation n fois de suite a une probabilité (1-p)exp(n)
la réalisation au moins 1 fois de l'évènement a une probabilité 1-(1-p)exp n mais si p et n sont petits c'est très proche de nxp
appliqué au cas de Sellig : p=0,001 et n=3
p=1-0,999exp3 = 0,002997 (et pas 0,003)
OK, on est très loin du poker là.
ven, 09/03/2012 - 08:56
#15
Koniflush a écrit :
Edit: ?? j'enlève pas de 5 dans les calculs! euh non je retire 2 cartes pour le calcul du joueur n+1. Prenons l'exemple du joueur 2, il a reçu un seul 5, quand tu vas calculer la proba pour le joueur 3, tu fais le calcul en sachant que 2 cartes non vues, ont été donné. L'une d'elle peut être un 5 ce qui donne au joueur 3 une probabilité de 0 d'avoir 55.
si tu retires deux cartes du deck pour le calcul du joueur N+1, et que tu re-calcules les combinaisons d'avoir 55 sur ce deck, ça veut dire implicitement que joueur N n'a pas de 5 !
ven, 09/03/2012 - 09:21
#16
pasdebol a écrit :
Arretez les gars, sellig07 vient de faire une embolie cérébrale
c'est vrai que son silence est inquiétant !
quelqu'un a des nouvelles
?
ven, 09/03/2012 - 09:46
#17
DynaX a écrit :
pasdebol a écrit :Arretez les gars, sellig07 vient de faire une embolie cérébrale
c'est vrai que son silence est inquiétant !
quelqu'un a des nouvelles
vous inquiété pas les amis, je suis vivant ni subit aucun dommage cérébral ( n'est ce pas Pasdebol ).
J'ai juste pas eu le temps de lire et d'étudier vos post.
Merci à vous.
ven, 09/03/2012 - 09:47
#18
kaliganzaris a écrit :
...la réalisation au moins 1 fois de l'évènement a une probabilité 1-(1-p)exp n …
pour moi, l’erreur dans ton calcul vient du fait qu’il inclus la possibilité que l’évènement se produise plus d’une fois (au moins une fois => 1 fois ou plus) ce qui n’est pas possible ici…
mais effectivement, dans la pratique, ça ne change quasiment rien au résultat et je reconnais que ma simulation sur l’ordi n’est pas assez précise pour mesurer l’écart qui est de (pour 20 joueurs)
(1 – 0.001*20) - 0.999exp(20) = 0.000189 (0.02%)
- Vous devez vous identifier ou créer un compte pour écrire des commentaires
elle ne dépend pas des des as et du 7 qui sont déjà sortis (mais uniquement des 5) et ne dépend pas non plus du nombre de joueurs qui ont callé
en revanche si la question est "quelle est la chance que Héro soit battu par une paire de 5", là il faut multiplier la probabilité précédente par le nombre de joueurs adverses, en l'occurrence 3/1000.
mais sinon, avec le tirage que tu donnes (aux couleurs des cartes près), Héro a environ 73% de chances de gagner le coup, et donc 9% pour chacun des 3 opposants, (ça c'est mon ptit calculateur de cote perso en python qui me l'a dit